Friction: static and dynamic
By Tyler Housel, Contributing Editor | TLT Lubrication Fundamentals August 2025
Does antimatter cause friction?

Nowadays, articles often use a tagline with an outrageous teaser so curious readers will click on the link. If the clickbait worked for this article, you may be disappointed to know that friction is not caused by antimatter. However, it is possible to model friction as a correction factor which acts like negative mass. In any event, antimatter has positive mass just like regular mass, and this was experimentally confirmed in 2023 by a team at the European Center for Nuclear Research (CERN).1
Newton’s laws of motion give an elegant description of inertia, forces and motions that accurately describe most of celestial mechanics. Einstein gained international fame with the theory of relativity that corrected Newton’s laws to include black holes and galactic lenses. But Newton’s original laws cannot be used here on Earth because they ignore friction. We tribologists must also correct Newton’s laws to deal with life on a frictional planet.
Early work on friction
Leonardo da Vinci didn’t need a five billion dollar particle accelerator to perform detailed investigations on friction back in the 15th century. Using wooden blocks, ropes and pullies, his two main conclusions (shown below) are remarkably accurate considering the limited range of conditions he could explore. And da Vinci’s work was two centuries before Newton developed the concept of force.
1. Objects of equal weight will have equal frictional resistance regardless of the length or breadth of the contact.
2. The friction produces double the amount of effort if the weight is doubled.2
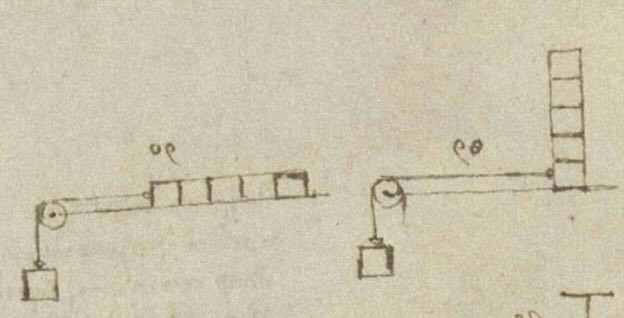
Figure 1. Excerpt from da Vinci’s notebook. Figure courtesy of Hutchings, I. (2016), “Leonardo da Vinci׳s studies of friction,” Wear, 360-361, pp. 51-66.
Figure 1 shows drawings from da Vinci’s notebook showing that friction depended on the total weight of the blocks rather than the way they are stacked. Surprisingly, he found that friction was independent of contact area, so it does not depend on pressure (force per unit area). This experiment showed da Vinci that friction is proportional to the downward (normal) force and eventually led to the equation here with the proportionality constant we know as the coefficient of friction (μ).
Ffriction= μFnormal
Coefficient of friction (μ)
Readers of TLT are familiar with the coefficient of friction (COF), which is represented by the lowercase Greek letter Mu (μ). It is widely reported at meetings and discussions with colleagues, and everyone knows that a lower COF implies better lubrication. Many tables are available online that list the COF for various material combinations. However, we do not include one in this article, and I strongly caution against treating μ as a constant because COF can vary with many factors such as speed, lubrication, load, lubrication, temperature, lubrication, surface roughness and lubrication. And did I mention lubrication?
COF is a useful concept, but it comes with a lot of caveats shown in Table 1. Laboratory test equipment is designed with a known geometry, so the machine easily calculates COF values. Please be aware that the terminology can be confusing as the “applied load” in a lab test often refers to the “normal force” rather than the “applied force.”
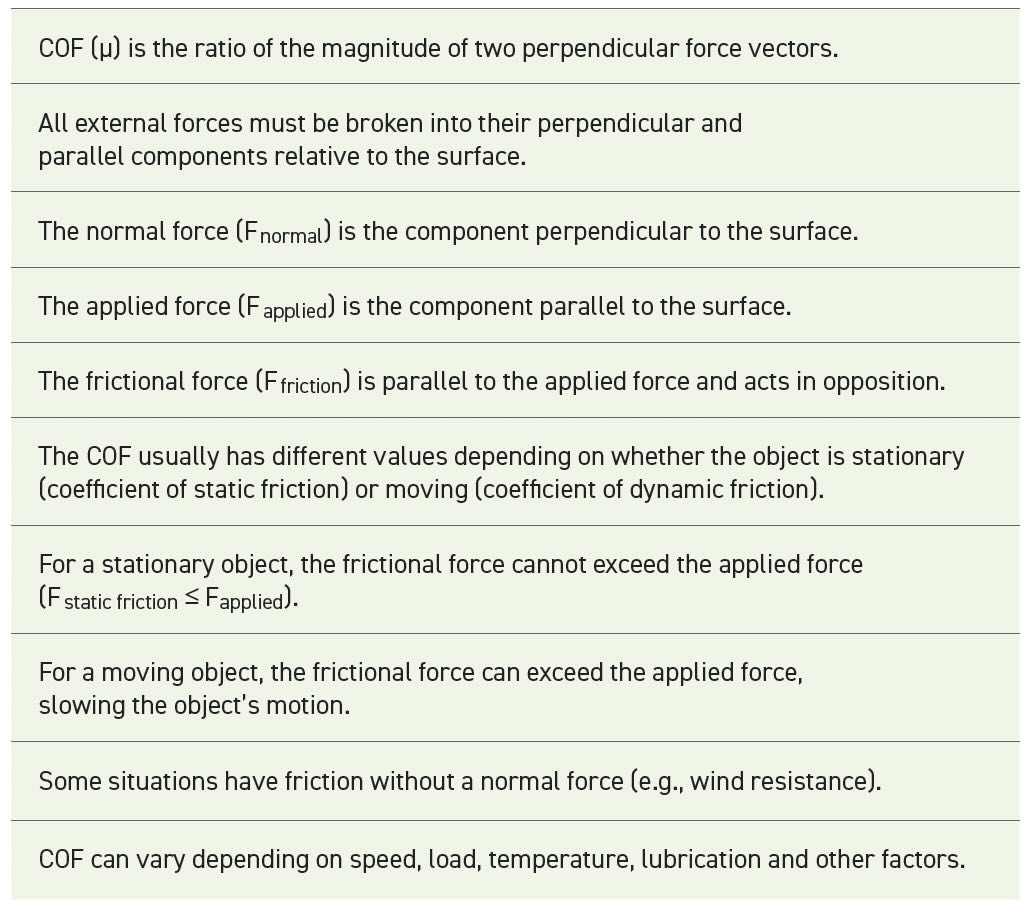
Table 1.
Using COF in real-world situations can be more complicated. To begin with, COF is a dimensionless (scalar) number that compares the magnitude of two perpendicular vector forces. Figure 2 shows an easy example with a flat, horizontal surface where the two forces are perpendicular. But if the surface is tilted at an angle (θ), the normal force is the weight (mg) times the cosine of θ. Meanwhile, the weight times the sine of θ is added to or subtracted from the applied force. Of course, it’s also possible that the applied force is not parallel to the surface, and similar trigonometric corrections must be included when calculating the COF.
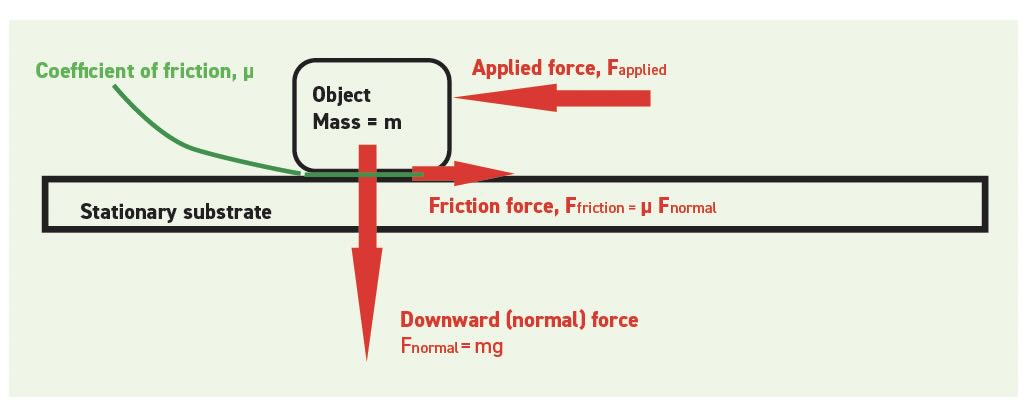
Figure 2. The arrangement of forces.
The next step in understanding friction is to distinguish between its two main types: static friction and dynamic friction.
Static friction
Consider again the object in Figure 2 sitting on a flat surface. Newton’s second law is given by the equation F=ma, which implies that a leftward applied force will cause an object at rest to accelerate in proportion to the inertial mass. But in truth, a stationary object will not accelerate unless the applied force is strong enough to overcome the frictional attraction between the object and substrate.
Even slippery surfaces have chemical attraction and microscopic surface asperities, and the peaks and valleys can interact with asperities on the countersurface. Movement only occurs if the applied force can break these microscopic bonds. We should note that static friction is a macroscopic phenomenon. The applied force must do something even if the object does not appear to move. Perhaps molecules are rearranged causing elastic or inelastic deformation. Or maybe the entire system (object + substrate) is accelerated while they remain stuck together.
If this article was appearing in “Adhesives & Sealants Industry” magazine,3 it would applaud the value of systems with high static friction. When we purchase picture hanging strips to mount a periodic table poster on a wall, the strip may say “holds up to 10 kg.” This means it has 10 kg (technically 98 Newtons) of static friction available to offset the downward pull of gravity. The friction always acts opposite the mass of the poster, so we can legitimately think that the friction provides up to -10 kg of mass. And note that in the vertical configuration, there is no normal force, so COF is meaningless.
Dynamic friction
The object in Figure 2 starts to move when the applied force exceeds the friction force. We can now use Newton’s second law to calculate acceleration after making a minor correction that accounts for friction as shown in the equation here. To add vectors, they must be parallel, and since the object is moving, this equation uses dynamic friction.
(Fapplied-Ffriction,dynamic)=ma
I was pushing my lawnmower and wondering why the continuous force applied to push the mower doesn’t lead to continuous acceleration. The mower briefly accelerates when you start pushing, but the speed quickly reaches steady state even though the pushing continues. Looking at the previous equation, it’s clear that a steady state condition exists when the applied force and dynamic friction force are equal. Lawnmowers, cars and even free-falling skydivers can achieve a “pseudo-inertial” state where the external forces are in balance. When the vector sum of all external force is zero, these objects will continue cruising in a straight line at a constant velocity.
In a true inertial system, there are no external forces, so an object’s motion remains constant (Newton’s first law). Just like true inertial systems, pseudo-inertial passengers inside a cruising airplane are moving at a constant velocity so they do not experience any additional forces related to their motion, but they still feel the force of gravity.
The main difference is that a pseudo-inertial object can change its motion without exerting a force by manipulating the friction forces that already exist. It just needs traction, so it has a way to affect the existing frictional forces. Airplane passengers cannot change the flight path because they don’t have traction with the outside air, but the pilot can maneuver using the different control surfaces on the airplane. Similarly, a skydiver can open a parachute and increase air resistance/friction significantly.
Traction
Traction comes from the frictional force between an object and the environment that allows them to exchange forces. Animals like fish, snakes and birds move by sliding, so their bodies are designed to efficiently manage dynamic friction using fins, scales and wings. A tree’s roots provide static friction to hold it tightly to the ground against the forces of gravity and wind.
Humans also rely on static friction because walking is a series of static contacts with the ground, and we can lose control if the foot slides unexpectedly. When we walk, our foot lands vertically on a spot and maintains contact with the same spot until it is lifted at the end of the step. During this time, we can transfer forces to the ground if we want to stop, speed up or change direction. If we attempt to accelerate too suddenly, the applied force may exceed the frictional force and our foot will slip. Detailed analysis of my walking shoes (see Figure 3) shows that wear occurs discontinuously on the sole. I assume the highest wear corresponds to areas where most force transfer occurs, and after years of walking the wear pattern becomes evident.

Figure 3. Wear patterns of shoes.
Humans have long realized that wheels are a useful way to move heavy objects with less effort. Whoever first developed the wheel probably didn’t think about the frictional or mathematical similarity between walking and rolling (see Figure 4). But both are a series of stationary contacts that use static friction to achieve traction with the ground. The main difference is that footsteps are discrete, and rolling is continuous. When sitting in a car, we might assume that the top and bottom of the tire both move at the same speed. But in fact, an observer on the ground will see that the bottom of the tire is not moving horizontally when in contact with the ground, while the top of the tire moves at twice the car’s speed. Therefore, tire traction is governed by static friction during this brief moment of stationary contact.

Figure 4. Wheels.
The total contact area between a car and the ground is about the same as a piece of notebook paper (0.06 m2).4 Despite this small contact area, modern tires are highly engineered to provide excellent traction during acceleration, steering and braking (whew, I almost wrote “breaking”) and must perform under a wide range of temperature and road conditions. In addition, they wear slowly and provide an efficient, quiet and comfortable ride to passengers. Static friction may not resonate with the general public, but everyone understands why the idiom “where the rubber meets the road”5 means the most critical part of a large enterprise.
REFERENCES
1. www.space.com/gravity-affects-matter-antimatter-similarly
2. Resnick, R. and Halliday, D. (1977), Physics, Part 1, 3rd Edition, John Wiley & Sons Inc., page 99.
3. www.adhesivesmag.com
4. Dr. Anurag Warhadpande, Bridgestone Tire Technology presentation to the Philadelphia STLE, January 16, 2025.
5. Also a song by Meatloaf, 1995.
Tyler Housel is a technologist for Hnuco Technologies and is based in Lansdale, Pa. You can reach him at tylerhousel@comcast.net.