Conservation of angular momentum
By Tyler Housel, Contributing Editor | TLT Lubrication Fundamentals July 2025
Linear momentum is straightforward, but angular momentum makes the world go round.

The beginning of an article is like a person standing on a 10-meter diving platform staring at the water below. Last month’s topic was linear momentum, which is a forward dive in the tuck position having a degree of difficulty (DD) of 1.4.1 This month is about torque, rotation and angular momentum, so we’re attempting a reverse 4 ½ somersault in the pike position (DD = 4.8). Can we stick the landing? Read on and find out.
Ignoring air resistance, the center of gravity of a diver (or any other object) in freefall follows a parabolic path determined by the initial velocity and gravity. After leaving the platform, there are no horizontal (x direction) forces, so the diver’s horizontal velocity is constant until hitting the water. Gravity acts in the vertical (z) direction causing a uniform downward acceleration of 9.8 m/s2, corresponding to a linearly increasing vertical velocity. The solid lines in Figure 1 show the x and z velocities and the dots are the distance traveled in each dimension during the 1.65 seconds it takes to complete the dive. Figure 2 shows the parabolic arc of a diver2 as seen by the viewer on TV.
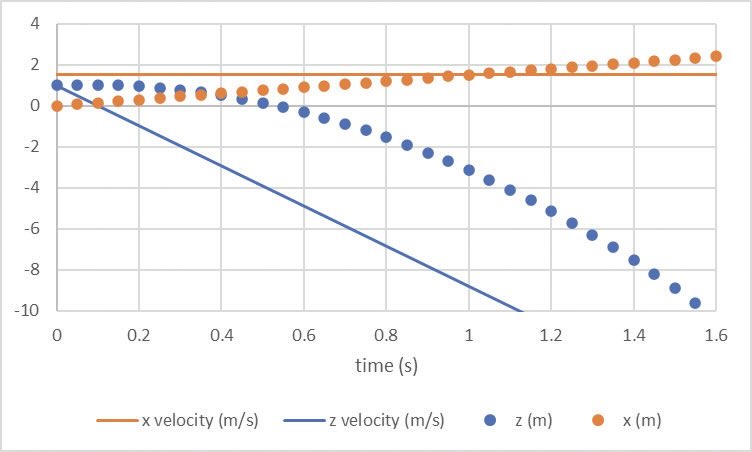
Figure 1. Velocity and distance of the center of mass when diving from a 10-meter platform.
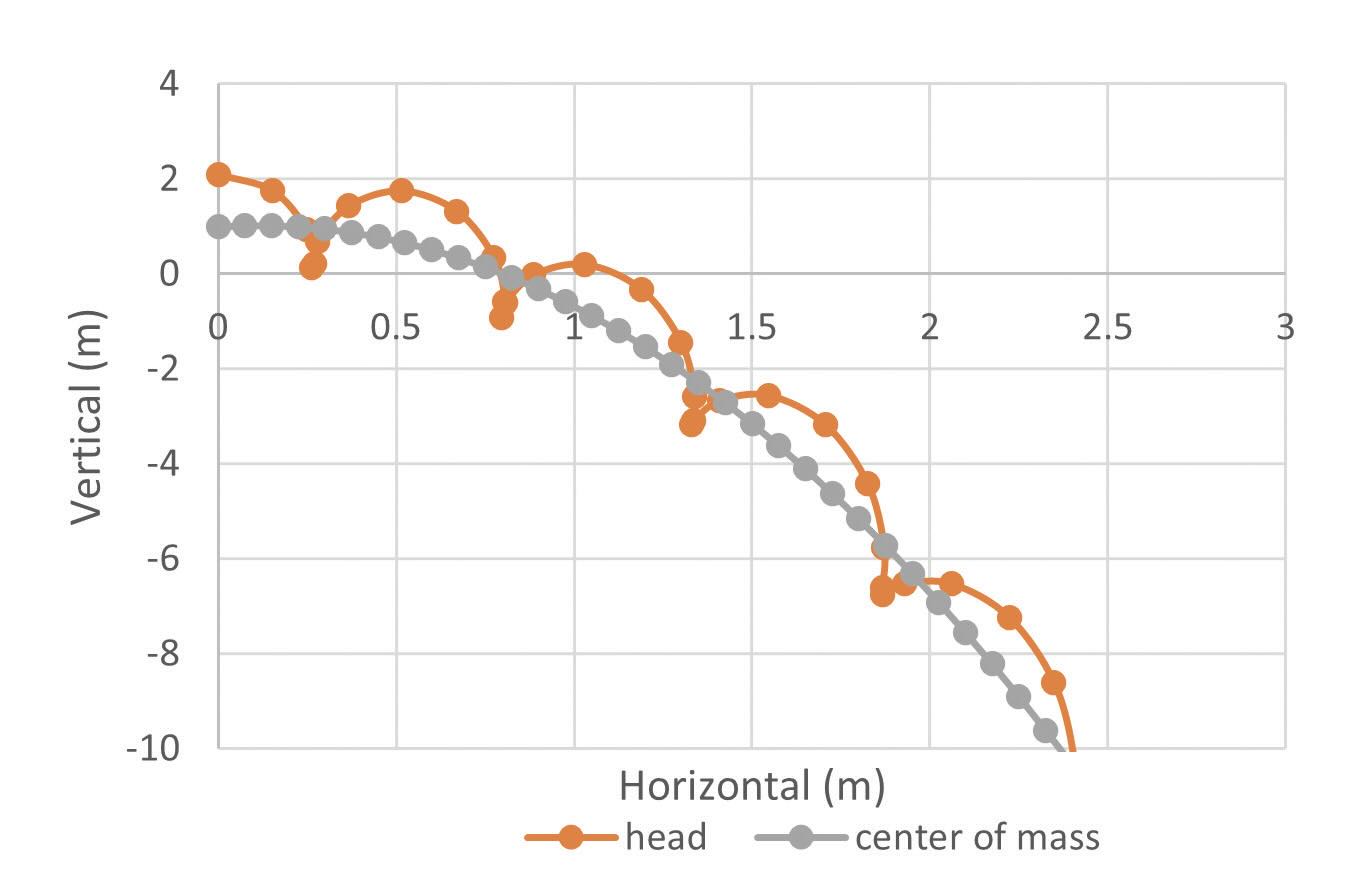
Figure 2. Path of the head and center of mass for a 4 ½ rotation dive.
Linear momentum and gravity cause all divers to follow the same parabolic path. The skill in platform diving comes from the ability to gracefully spin and twist while falling toward the water. Divers must have an inherent feel for their rotational motion, while physicists use advanced mathematical tools and Greek letters to explain the underlying laws. Tribologists often encounter rotating systems, and STLE recently held an Industry Insights discussion on rotational dynamics.3
The diver starts at rest and intuition tells us that the force applied by the feet against the stationary platform will push the diver linearly away from the platform and may also cause the diver to rotate. It would be very complicated to measure the linear and rotational motion in a single calculation, so physicists divide the motion into two frames of reference as shown in Figure 2. The first reference frame is the freefall motion of the center of mass (CM) according to the standard force equations shown by the gray line. The second reference frame is pure rotation and assumes that the CM is fixed in space. Finally, we calculate the motion of the diver’s head by adding the rotational and linear vector components with the looping path shown in orange.
Linear motion is relatively simple because it usually assumes all the mass of an object is concentrated at the CM and all forces act linearly on that point. Newton’s three laws of motion implicitly apply at the CM.
Rotational motion is more complicated because it requires at least two masses (M1 and M2) separated by a distance (2R) and the masses must be bound together by a force that keeps them together as they spin around a common axis. This centripetal force is necessary to counteract the tendency for each object to follow its straight-line inertial path, so it coordinates the motion of the two masses into a single system.
Let’s model the diver as a simple two-dimensional rotating dumbbell as shown in Figure 3. I don’t mean to imply Olympic divers are dumbbells, but you would never catch me jumping off a 10-meter platform. This dumbbell has two 1-kilogram masses (M1 = M2 = 1 kg) separated by a 2-meter-long massless rod with a fixed axis of rotation at the CM, which is halfway between the masses, so R1 = R2 = 1 m. In the rotational frame of reference, we will ignore air resistance and assume gravity can be ignored because it affects both masses equally. Therefore, the dumbbell can spin freely, and the masses will always remain on the circular path in the plane of the paper.
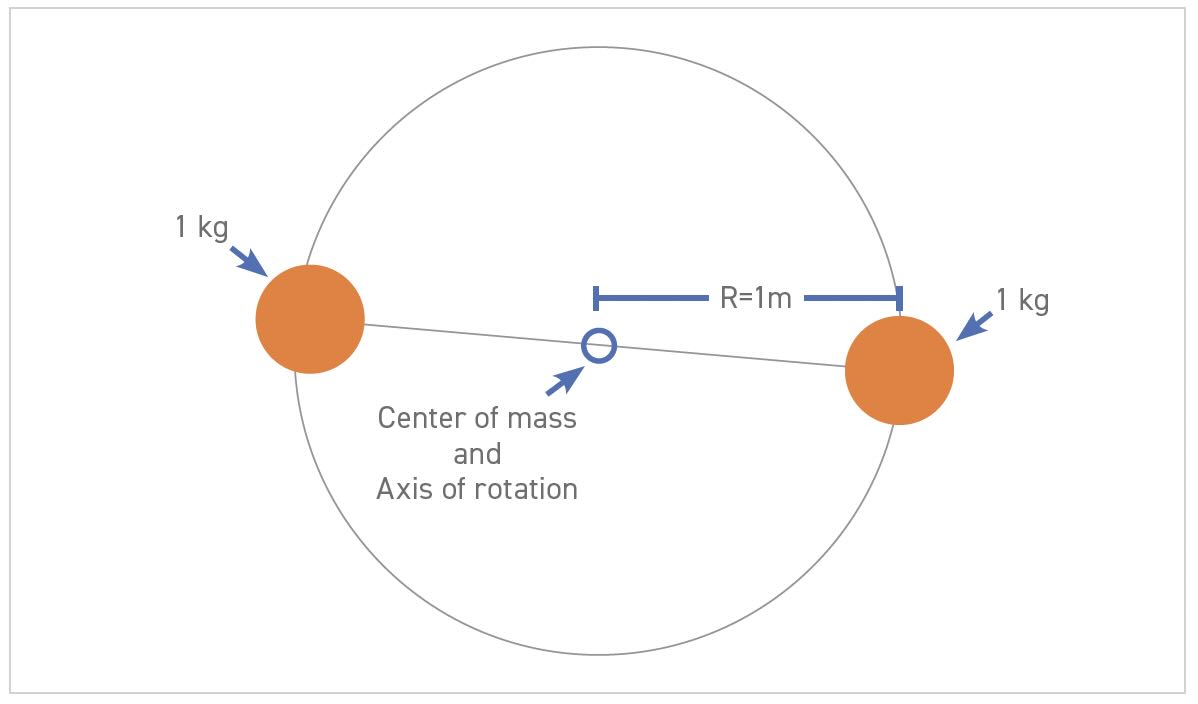
Figure 3. Dumbbell.
We already understand linear motion from previous articles,4 so this is a convenient starting point for rotational motion. But instead of distance, velocity and acceleration, we measure rotational angle, angular velocity and angular acceleration. Recalling high school trigonometry, the SI base unit of angle is a radian (rad), which is the length of the circle’s radius transcribed around the circumference. Readers may be more familiar with degrees, so the conversion is shown in Figure 4. One radian gets us about 57 degrees around the circle because the circumference of a circle is 360 degrees or 2π radians. Table 1 shows the similarities between linear and angular measurements.
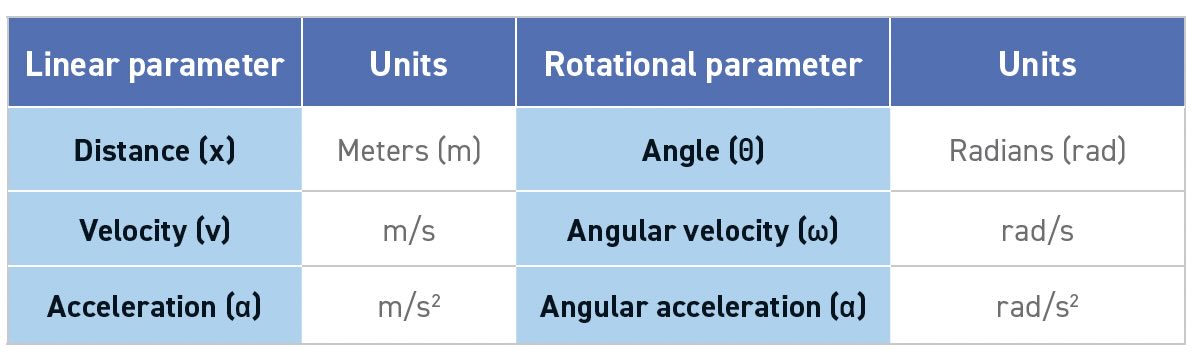
Table 1.

Figure 4. Radians.
Torque (τ) and force (F)
Torque only occurs when a force interacts with an object at a point distant from the axis of rotation. Torque is the tangential component of the force times the radial distance (F⊥ x R) and is calculated as the vector product of the force and distance vectors. The magnitude of the torque is determined by multiplying the magnitudes of the distance and force vectors times the sine of the angle between the two. The direction of the torque vector is perpendicular to both other vectors, so it points out of the page. Vector products are also known as cross products so the “x” in the equation below is a “cross.” Interested readers can learn more about vector products online.5
torque τ=RxF=RF sin ø
Each end of the dumbbell is 1 m from the axis of rotation, so a 1 N force on one end can produce a torque of 1 Nm if the distance and force vectors are perpendicular (sin 90° = 1). A force vector cannot induce spin if it intersects with the axis of rotation (sin 0° = 0). You may have noticed that torque is measured in Newton meters which can be a unit of energy (Joules= N m). However, torque and energy are different concepts, and one important distinction is that torque is a vector and energy is a scalar. Vector math may be unfamiliar but torques are convenient because the magnitude and direction of the torque do not change as the dumbbell spins on its axis.
Archimedes anticipated the concept of torque when he famously said, “Give me a place to stand and I will move the Earth.” He recognized that a heavy load can be moved with a small force that is applied far from the fulcrum (axis of rotation). The lever principle means that two objects are in balance when the torques are equal and opposite (see Figure 5).
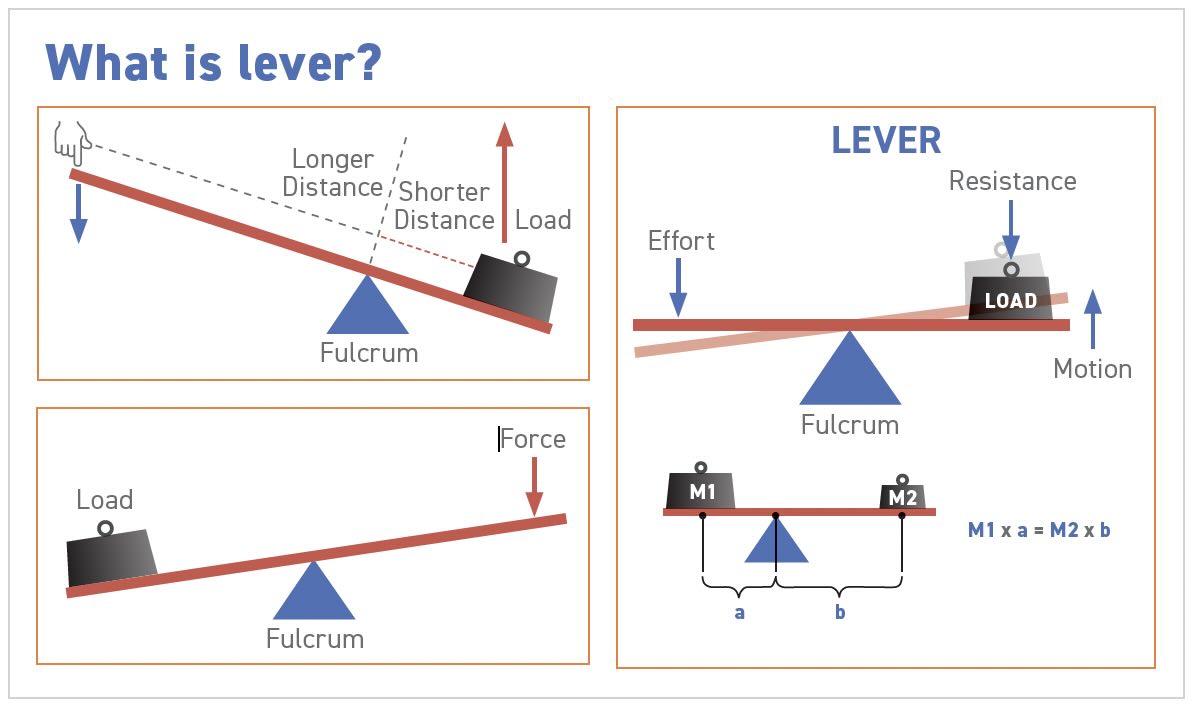
Figure 5. The lever principle.
Rotational inertia (I) and inertial mass (m)
Newton’s laws of motion state that objects will remain in an inertial (unchanging) state of linear motion unless acted upon by an outside force. The same holds true for rotational motion, with torque and angular acceleration taking the places of force and linear acceleration. The rotational inertia, sometimes called the moment of inertia, relates torque to angular acceleration (τ=Iα) in the same way that mass is used in Newton’s equation (F=ma) as shown below. The torque and angular acceleration vectors are always parallel and point out of the page, so it is not necessary to include a sine or cosine function.
Inertial Mass m= force/(linear acceleration)=F/a
Rotational Inertia I=torque/(angular acceleration)=τ/α
We can measure the rotational inertia experimentally from torque and angular acceleration, but it is usually easier to calculate the rotational inertia from the mass and distance of elements that make up the system. The rotational inertia of each element is the mass times the square of the radial distance, and we get the total rotational inertia by adding (integrating) all the elements that make up the system as shown below.
The freefalling dumbbell only has two elements, and each has a mass of 1 kg at a distance of 1 m from the axis of rotation, so the calculation is simple. The rotational inertia of one element is 1 kg m2 (MR2) so the total for both is 2 kg m2. Please note that this is only correct because the axis of rotation is halfway between the two ends.
Itotal=∫R2 dm=(1 kg)(1 m)2+(1 kg) (1 m)2=2 kg m2
However, a diver has a more complicated mass distribution with many elements (arms, legs, head, torso, etc.) at various distances from the axis of rotation. They can also bring their body parts closer to the axis of rotation (=CM) which will change the rotational inertia even while in the air.
Linear momentum (p) and angular momentum (L)
Last month’s TLT Lubrication Fundamentals article6 covered linear momentum, which is defined by the equation p=mv. Using our angular substitutions, we define angular momentum as L=Iω. Angular momentum is extremely useful because it also has a robust conservation law, which allows physicists to describe the behavior of everything from subatomic particles to the structure of galaxies. The conservation of angular momentum even applies in relativistic and quantum realms where Newton’s laws of motion break down.
The diver must complete exactly 4 ½ rotations in the 1.65 seconds between launch and splashdown which means an average angular velocity of 2.73 rotations per second or 17.14 rad/s.
average angular velocity (ω)=(4.5 rotations)/(1.65 seconds)=(4.5 x 2π rad)/(1.65 s)=17.14 rad/s
After leaving the platform, the mass, horizontal velocity, gravity, linear and angular momentum are all constant. You might assume that everything is predestined as soon as the diver begins to freefall, but a diver (unlike a dumbbell) can fine tune the rotations in mid-air. The angular velocity is inversely proportional to the rotational inertia (ω=L/I), and this is determined by the distribution of mass around the axis of rotation. By bringing the legs and head closer to the torso, the rotational inertia decreases which increases the spin rate. A skilled diver knows exactly when to come out of the tuck and extend the arms and legs to slow their rotation and make a perfect, vertical entry into the water. And divers do all of this while pointing their toes. It’s an incredible feat and I’m always impressed.
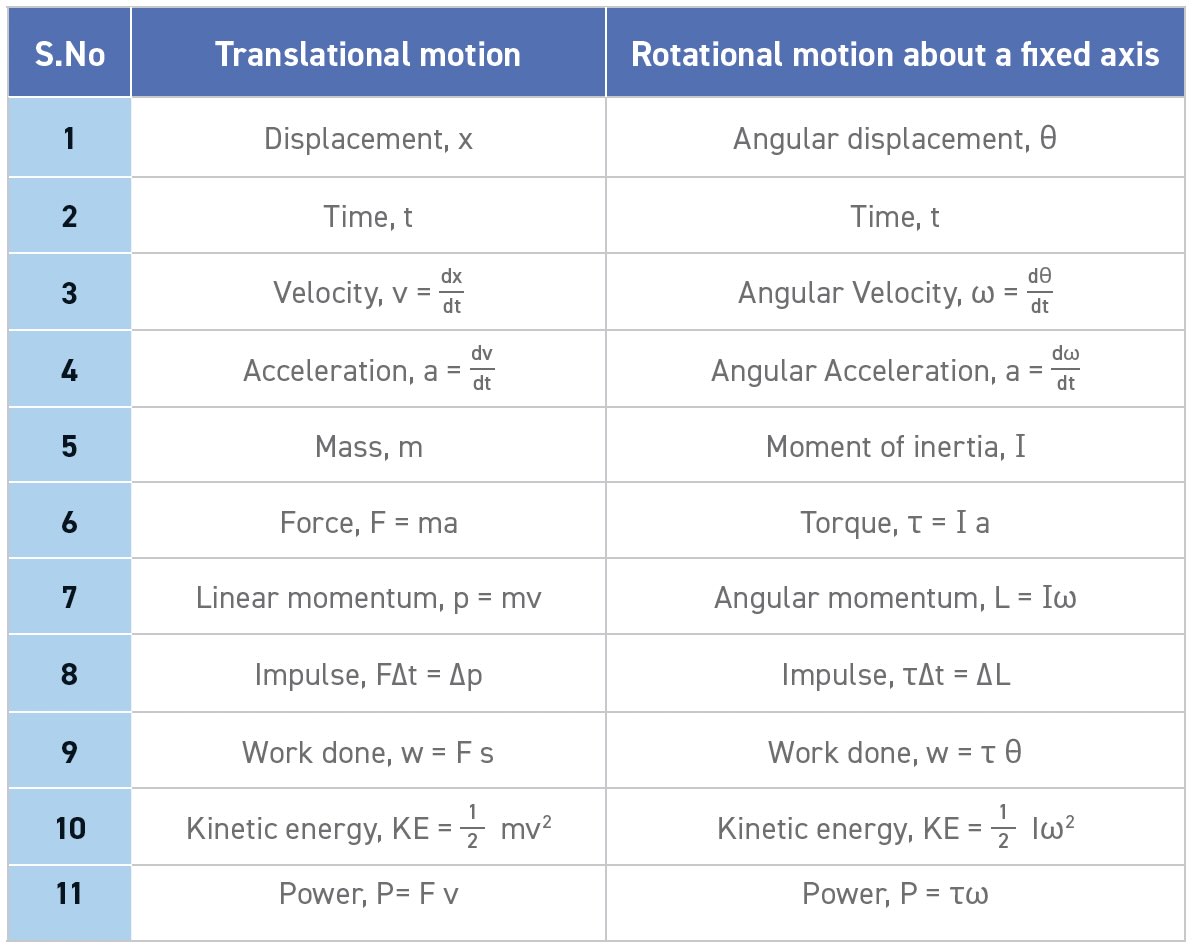
Table 2. Comparison of translational and rotational quantities
Summary
Table 2 summarizes the analogous relationships between linear and rotational motion. There were 59 pages in my freshman physics book7 devoted to the basics of rotational dynamics. These concepts were then applied throughout the next 1,000 pages to explain many important topics in physics. This article only scratched the surface, but fortunately, there are multiple sources for advanced study and many experts in the STLE community who can multiply vectors in their sleep (but they probably don’t read Lubrication Fundamentals). I hope the diving analogy helped make the topic less abstract for those with a more modest appreciation of physics.
REFERENCES
1. https://diving-gbdf.com/downloads/fina-dd.pdf
2. No relation to the Steve Winwood song “Arc of a Diver.”
3. “Rotordynamic Tutorials,” STLE Industry Insights, April 24, 2025.
4. Housel, T. (2025), “The metric system,” TLT, 81 (5), pp. 28-32. Available at www.stle.org/files/TLTArchives/2025/05_May/Lubrication_Fundamentals.aspx.
5. www.geeksforgeeks.org/dot-and-cross-products-on-vectors/
6. Housel, T. (2025), “Linear momentum,” TLT, 81 (6), pp. 42-46. Available at www.stle.org/files/TLTArchives/2025/06_June/Lubrication_Fundamentals.aspx.
7. Resnick, R. and Halliday, D. (1977), Physics, Part 1, 3rd Edition, John Wiley & Sons Inc.
Tyler Housel is a technologist for Hnuco Technologies and is based in Lansdale, Pa. You can reach him at tylerhousel@comcast.net.