Linear momentum
By Tyler Housel, Contributing Editor | TLT Lubrication Fundamentals June 2025
Friction can be viewed as a consequence of the law of conservation of linear momentum.

In physics, conservation laws describe quantities that remain constant when a system undergoes change. This article will start with Newton’s laws of motion and show how the conservation of linear momentum leads to air resistance, dynamic viscosity and friction. William Shakespeare often foreshadowed the ending of a play at the very beginning to build dramatic tension.1 Other comparisons to Shakespeare are unfounded, but if it’s good enough for the Bard of Avon, it’s good enough for TLT. Maybe next month’s Lubrication Fundamentals article will be written in iambic pentameter.
Imagine that the universe contains only a very dense 2 kilogram (kg) sphere sitting atop a massless infinite flat plane marked off with two sets of perpendicular lines that are spaced 1 meter (m) apart. The object sits at the intersection of two lines, and we can assign the directions as x and y. This creates a Cartesian grid with the object at the origin (x=0, y=0). For simplicity, all force and motion will occur in the x dimension, so we can treat the following examples as a one-dimensional world with y=0.
If we apply a force of 2 Newtons (N) to the mass in the +x direction for 1 second, the sphere will accelerate at 1 meter per square second (1 m/s2) according to the second law relationship F/m=a. After the force is removed, it will continue to move at 1 m/s in the +x direction forever. Figure 1 shows the relationship between acceleration (a), velocity (v) and distance (x) as well as the applied force (F) and momentum (p) as a function of time for the first few seconds after the force is applied. Newton’s second law shows a direct relationship between the parameters; doubling the force (or halving the mass) will double the object’s acceleration, velocity and momentum.
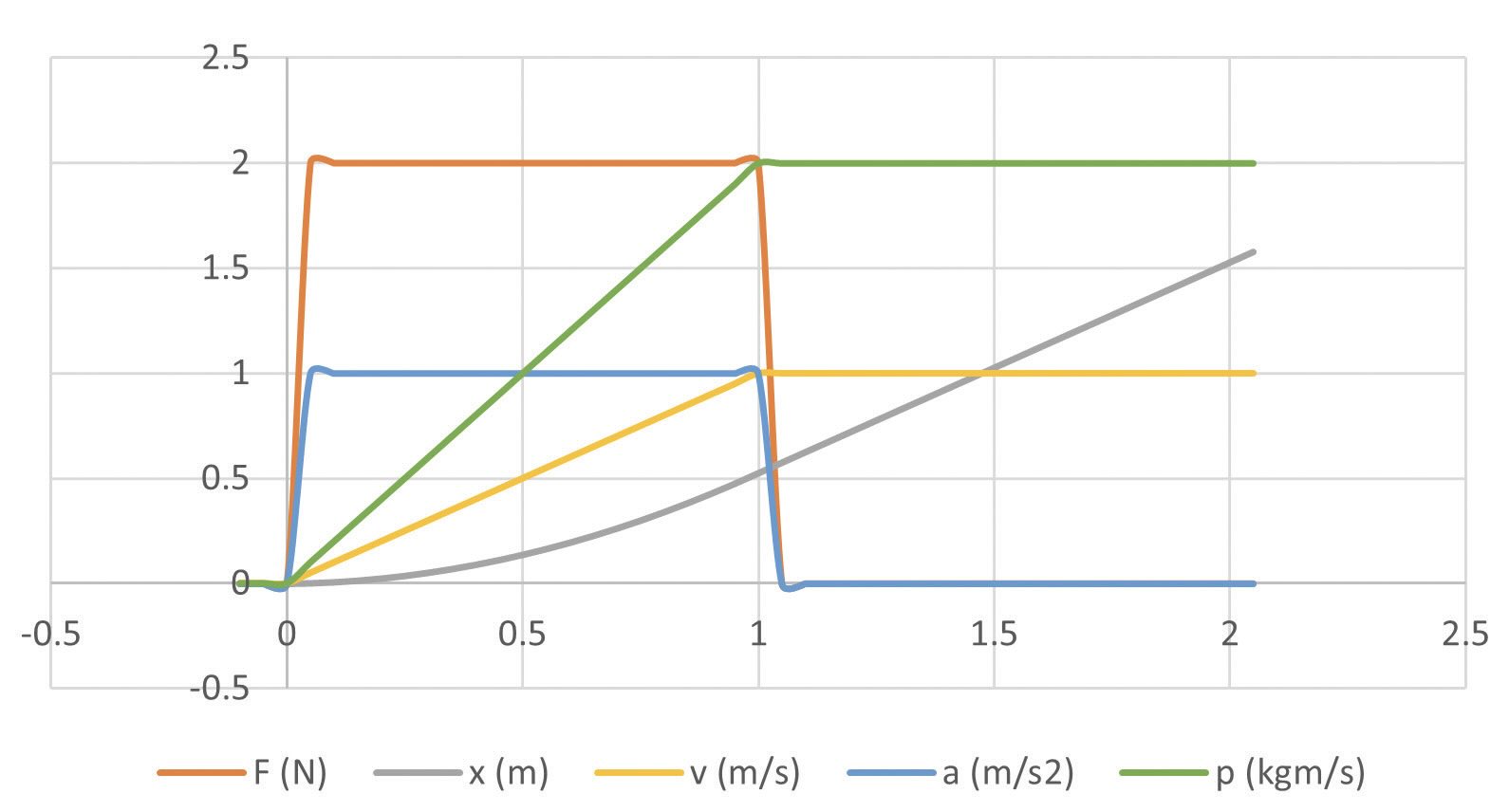
Figure 1. Motion of a 2 kg object plotted versus time.
Linear momentum
Linear momentum is a vector quantity defined as the mass times velocity (p=mv) with momentum represented by the letter “p.” You might notice that there is no “p” in the word momentum and there are different opinions about the origin of the p. Momentum is also the only basic unit that isn’t named after a famous scientist like force (Newtons), energy (Joules), power (Watts) and pressure (Pascals). In sports, someone has momentum when playing at their highest level, so perhaps we can name the unit of momentum after the most valuable football player in the championship game. Thus, momentum would be measured in (Jalen) Hurts,2 which also makes sense because a punch in the nose hurts due to the momentum of the fist. The only problem is that people could confuse Hertz (1/s) and Hurts (kg m/s). Maybe this isn’t a good idea after all.
Kinetic energy
Kinetic energy (KE) describes the energy of an object that results from its motion. Kinetic energy can be measured either as a force applied over a distance (KE = F x d) or as half of the mass times the square of velocity (KE = ½ mv2). Both calculations show the kinetic energy of the object is 1 Joule as shown below.
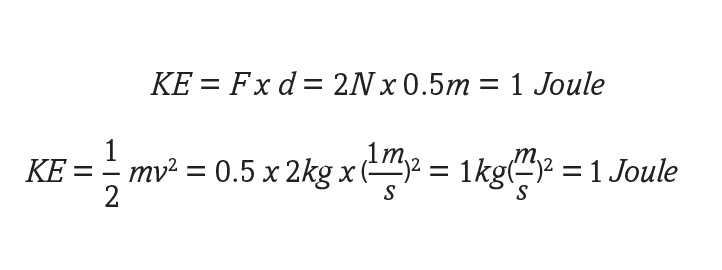
Conservation of linear momentum
The first object (Object A) has a total momentum of +2 kg m/s. Now we introduce a second object on a collision course with the first. Object B has a mass of 4 kg and a velocity of -2 m/s along the x direction resulting in a momentum of -8 kg m/s (negative velocity meaning that its motion is in the opposite direction). The two bodies define a system with a total momentum of -6 kg m/s. There are several possible ways the particles can interact, but the total momentum of the system will always remain constant. The conservation of linear momentum is a vector law so it applies to both the magnitude and direction. In these examples, all momentum is in the x dimension. If one object deflects in the y dimension, the other object must deflect in the -y dimension, so the total momentum in the y dimension remains zero.
Figure 2 shows an elastic collision between Object A and Object B. Momentum (8 kg m/s) and energy (8 J) transfer from one object to the other in such a way that the total momentum and kinetic energy of the system is unchanged. As a result, Object B stops and Object A is thrown backward at a high rate of speed.
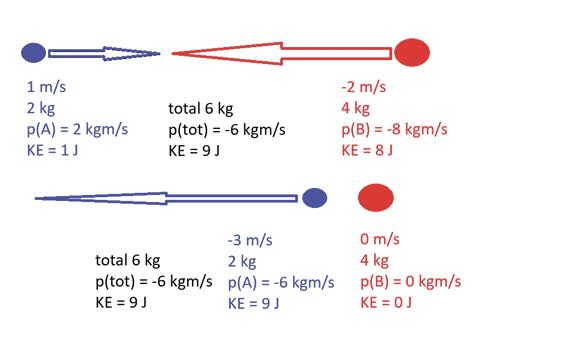
Figure 2. Elastic collision between Object A and Object B.
Conservation of energy
The velocity of each object changes when they collide, which means some period of acceleration must occur during the interaction. And acceleration requires internal forces on the atoms within the objects. If the atomic structure is resilient, it can reversibly bounce back to the pre-collision state and return all energy to the system as kinetic energy. Energy conservation is a universal law, but kinetic energy is just one form of energy. An elastic collision is a special case where kinetic energy is conserved.
When real objects collide, some kinetic energy is always lost. Figure 3 shows the extreme case of a purely inelastic collision where the two objects stick together. They absorb as much kinetic energy as possible, converting 6 Joules of kinetic energy to other forms of energy such as structural deformation and heat. This is why cars are designed with inelastic crumple zones instead of elastic bumpers so the car will absorb as much energy as possible in a collision (see Table 1).
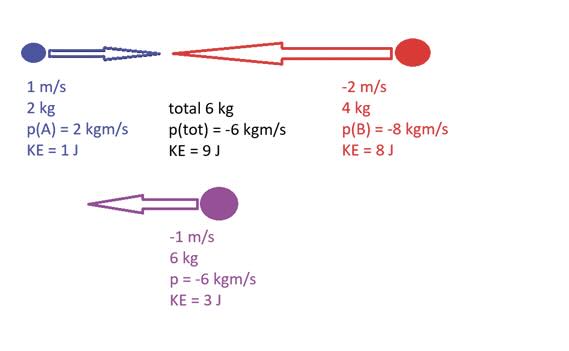
Figure 3. Inelastic collision where Objects A and B stick together.
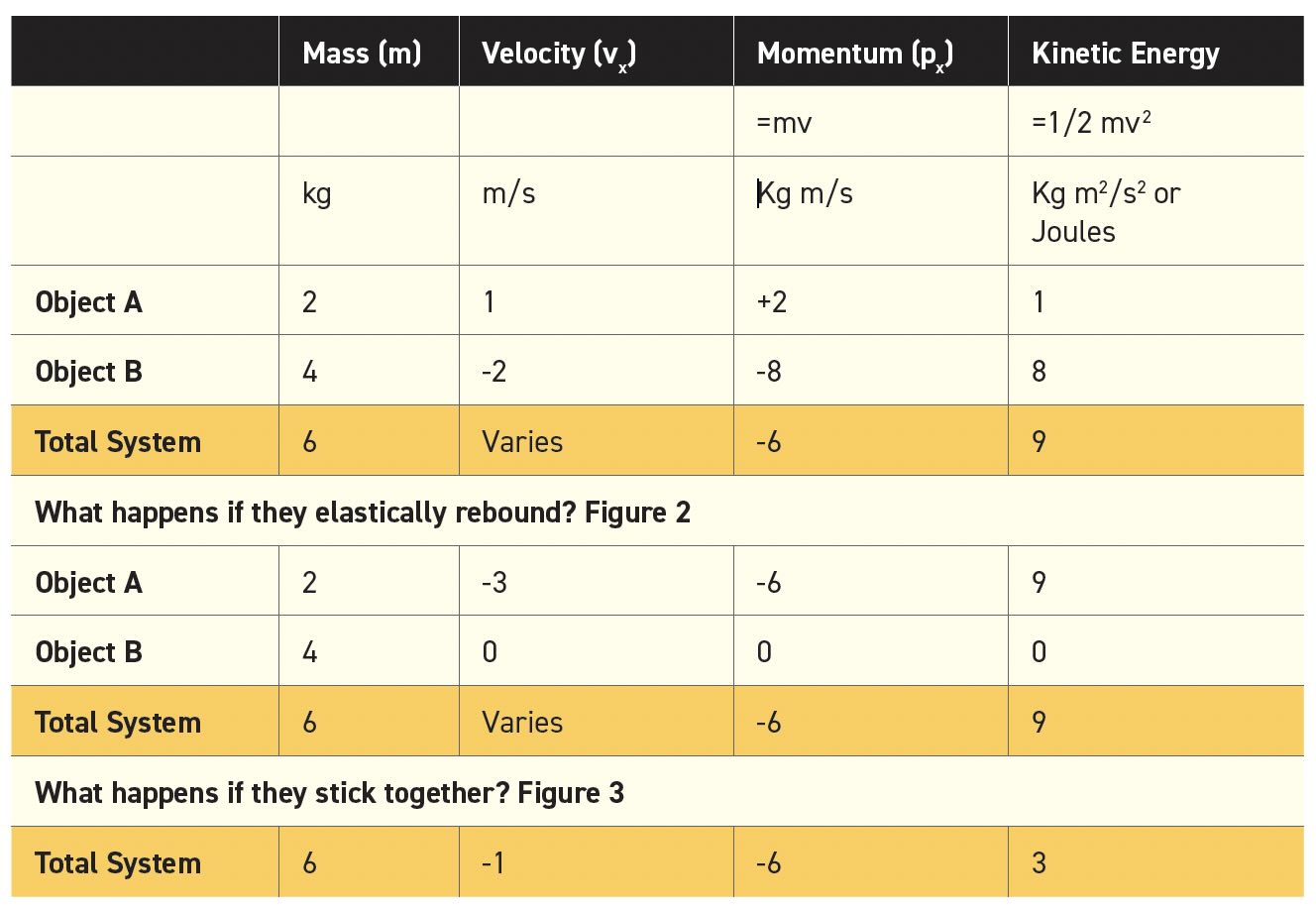
Table 1. Summary of momentum and kinetic energy for one-dimensional collisions
Air versus vacuum
Although we started with an infinitely large universe populated by only two objects, this is only realistic in the vacuum of space. Earth’s atmosphere has a very large number of very small particles moving in all directions. Every air molecule carries momentum which is the product of its mass and velocity. We can safely assume the momentum of each air molecule is very small relative to the moving object. But the quantity of air molecules and number of collisions is so large that it has a macroscopic effect on objects traveling through the atmosphere. It is not necessary to measure the speed and velocity of each individual air molecules. All the important information is captured by knowing the wind velocity, air pressure and temperature.
When a meteorologist says the winds are coming from the west at 3-4 m/s (7-9 mph), they are reporting a vector (magnitude and direction), which relates to the average vector momentum of the air molecules. Sailboats are engineered to convert the momentum of the air molecules into momentum of the boat. Windmills can use this momentum to pump water, grind grain or even convert it to electrical energy.
On a still day, the average momentum and velocity vectors are zero, but each individual molecule is still moving and carries momentum. Unlike wind velocity, air pressure is a scalar that measures the average magnitude of the momentum without differentiating the direction of motion. Static air pressure is the same in all directions. However, when the object’s motion is fast enough to create a pressure differential, then we must use Bernoulli’s equation to add the static and dynamic pressure.3
The average speed (scalar) of molecules in a gas is also directly related to temperature. Thermodynamics teaches that temperature measures the average KE of a population of molecules in an ideal gas. For each molecule, KE = ½ mv2. Atomic mass is not a function of temperature, so temperature is proportional to the square of the average velocity. Directionality is lost when calculating the average of a square function because all squares are greater than zero. So, temperature measures the average speed even when the wind velocity is zero.
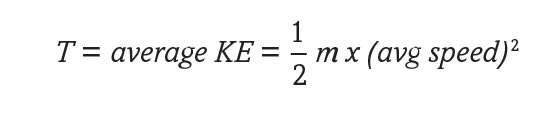
Air pressure and temperature are both ways to measure the average speed of a collection of individual gas molecules, so it isn’t surprising that the ideal gas law shows a direct proportionality between the two.
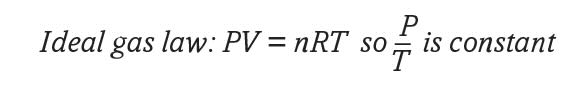
Air resistance
Figure 2 shows that an object can be completely stopped by an elastic collision with a smaller body as long as momentum is conserved. The same principle applies if we replace a single Object A with a large number of much smaller objects; Object B will come to rest as long as the sum of all collisions reduces its momentum to zero.
Any object in Earth’s atmosphere is constantly bombarded by air molecules. Figure 4 shows a large red object moving left in a sea of air molecules that are randomly moving both left and right. Each elastic collision transfers momentum. Collisions with (blue) rightward molecules reduce the momentum of the object. But some (blue) leftward molecules are moving slower than the object itself so these collisions also reduce the object’s momentum. Only a few very fast leftward molecules shown in red can increase the object’s momentum. The faster the object moves, the more resistance it encounters. Remember this next time you are hurrying to get to the airport.
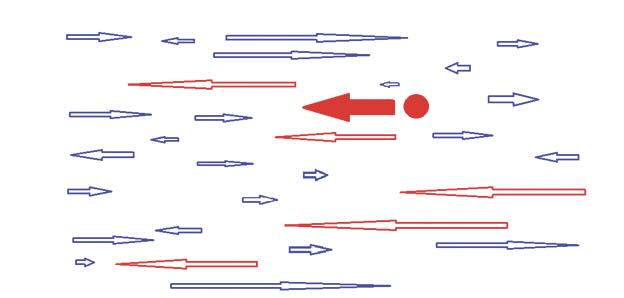
Figure 4. Red object moving through a population of air molecules.
The system eventually reaches equilibrium when the leftward and rightward collisions balance and the object velocity matches the average velocity of the air. Of course, the leftward wind velocity has increased because the air gains the leftward momentum that is lost by the object.
Momentum transfer in liquids
When tribologists measure dynamic viscosity with a rotational, parallel plate viscometer (i.e., Brookfield), the viscosity is the ratio of shear stress to shear rate and is measured in Pascal seconds (Pa s). A motor drives the top plate at a given velocity and the viscometer configuration maintains a known fluid thickness as shown in Figure 5.4 The gradient provides the shear rate. Shear stress is calculated from the motor torque required to drive the top plate at the desired velocity. The ratio (accounting for geometrical factors) provides dynamic viscosity.
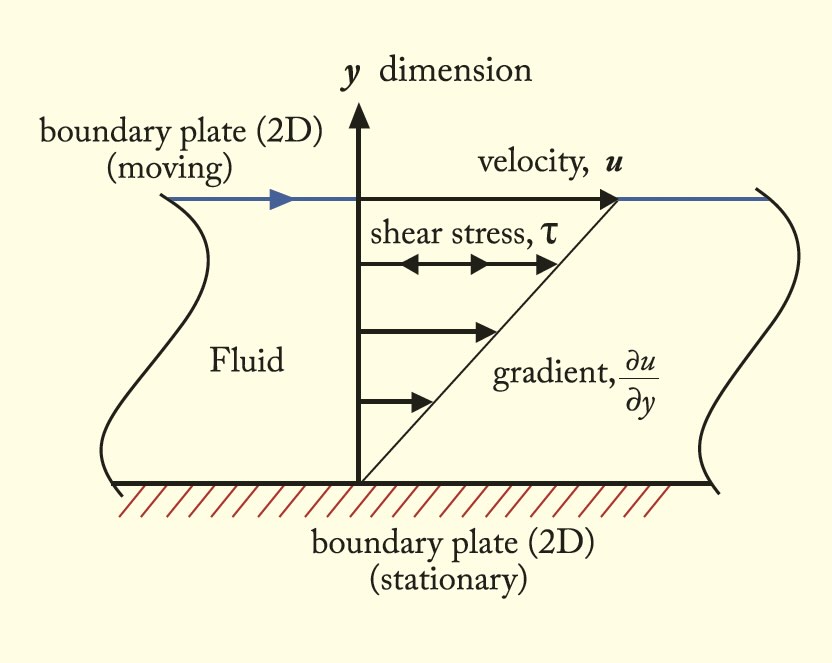
Figure 5. Laminar fluid flow in two dimensions. Note that this figure uses “u” for velocity instead of “v.” Figure courtesy of Duk at the English-language Wikipedia, CC BY-SA 3.0, via Wikimedia Commons.
An alternative way to understand viscosity is that it measures momentum transfer across a surface. Referring again to Figure 5, each layer moves slower than the layer above, so the momentum of each layer is also successively lower. Shear stress is the amount of momentum flow per unit area and the dynamic viscosity (Pa s) is the equilibrium momentum (kg m/s) differential per unit area (m2) between surface layers.
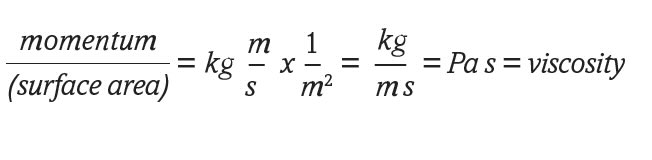
Friction
For millennia, no one seriously questioned Aristotle’s postulate that motion was unnatural and temporary; his natural laws required all inanimate objects to come to a state of rest (Aristotle’s Fallacy).5 Aristotle’s Fallacy was unchallenged because it matches everyone’s experience.
Newton’s classical laws of motion showed that moving objects remain in uniform motion unless some external force acts on them. Aristotle did not realize that the ground beneath our feet is in an inertial state of motion and all Earthly objects come to equilibrium by transferring excess momentum to the environment until they match the Earth’s motion. Tribologists perfect motion by managing the inevitable loss of momentum, allowing equipment to approach its ideal inertial efficiency.
REFERENCES
1. https://brainly.com/question/28045014
2. www.usatoday.com/story/sports/nfl/super-bowl/2025/02/09/jalen-hurts-named-mvp-super-bowl-59/78378632007/
3. https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/air-pressure/
4. Housel, T. (2025), “The metric system,” TLT, 81 (5), pp. 28-32. Available at www.stle.org/files/TLTArchives/2025/05_May/Lubrication_Fundamentals.aspx.
5. Housel, T. (2025), “Calculation or experience,” TLT, 81 (1), pp. 24-27. Available at www.stle.org/files/TLTArchives/2025/01_January/Lubrication_Fundamentals.aspx.
Tyler Housel is a technologist for Hnuco Technologies and is based in Lansdale, Pa. You can reach him at tylerhousel@comcast.net.