Modeling hydrogel friction
Drs. Wilfred T. Tysoe & Nicholas D. Spencer | TLT Cutting Edge October 2018
Analytical models show how adhesive and viscous effects account for their velocity and load dependencies.
Mucus, which is made up from interlinked networks of proteins and polysaccharides that incorporate large amounts of water, is used in nature to lubricate the mouth, intestines and eyes. Its tribological properties are often measured using structurally similar hydrogels, which also consist of cross-linked polymers that contain large quantities of water so they are soft and viscoelastic. As a consequence, their frictional properties have been extensively investigated and have shown remarkable differences in behavior. For example, hydrogel friction has been found to increase, decrease or be independent of normal load and of sliding velocity. While there have been a number of phenomena invoked to explain this disparate behavior, up until now there has been no comprehensive model for hydrogel friction.
This has been addressed by professor Rosa Espinosa-Marzal of the University of Illinois at Urbana-Champaign, who modeled the frictional behavior of silica beads of 20 and 5 μm in diameter when sliding on polyacrylamide (PAAm) hydrogels with three different compositions as a function of load and by varying the sliding velocity by four orders of magnitude from 0.5 to 500 μm/s to yield typical results shown in Figure 1.
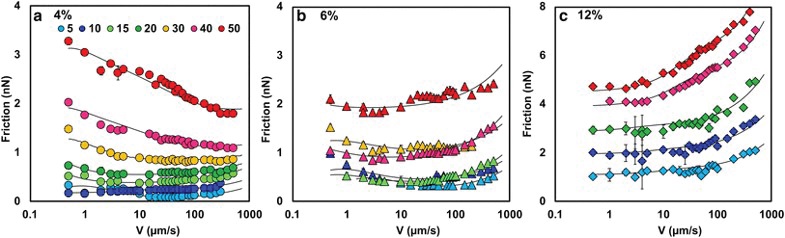Figure 1. Friction force as (a) a function of the sliding velocity for a 4% (circles), (b) 6% (triangles) and (c) 12% (diamonds) PAAm hydrogels at the following normal loads: 5 (light blue), 10 (dark blue), 15 (light green), 20 (dark green), 30 (yellow), 40 (fuchsia) and 50 (red) nN. The elastic moduli of the three hydrogels are (a) 1.8 ± 0.9, (b) 9.9 ± 0.2 and (c) 12.9 ± 1.3 kPa, respectively. There is a quantitative agreement between consecutive loops, which is reflected in the small error bars (often smaller than the symbol size and therefore not visible), indicating that the hydrogel deformation is reversible, i.e., the hydrogel fully recovers during the measurement of each loop. The black lines give the calculated friction force. Colloid diameter = 20 µm. Spring constant = 0.4 N/m. Note the different scales on the Y-axis of (c). (Published with permission from Ref. 1.)
An analytical model was developed that included three effects. The first was due to an adhesive friction force,
Fadh. This was described by a model first proposed by Schallamach for rubber friction, where frictional energy is dissipated by stress-activated bond cleavage and formation at the sliding interface. This is expected to yield a friction force that varies approximately as v
-0.1 with velocity,
v.
The second effect was proposed to be due to viscous flow of the hydrogel film, where the possibility of non-Newtonian behavior was included by incorporating a non-linear strain-rate dependence. Finally, an empirical quasi-velocity independent friction term
F0 was added to take account of the observation that the friction does not decrease to zero at very low velocities. The model was then tested by simultaneously fitting the analytical equations to all the data, and the results are shown as solid lines in Figure 1.
In particular, the fit revealed a strain-rate exponent for the viscosity between -0.3 to -0.35 for data collected at higher sliding speeds; the hydrogel film shows shear-thinning behavior, implying that the friction force should show an approximate v
0.3 dependence.
The proposed velocity dependences for the adhesive and viscous components of friction were tested by plotting F/F
min, where F
min is the minimum value of the friction force versus normalized velocity, V/V* (
see Figure 2). This reveals that all the data collapse onto a single curve where the friction at low velocities varies as approximately v
-0.1 as expected for adhesive friction and as v
0.3, as expected for viscous friction. A deviation was observed for some experiments at low loads (
m~0.5), which was tentatively associated with the lack of confinement of the polymer under small loads.
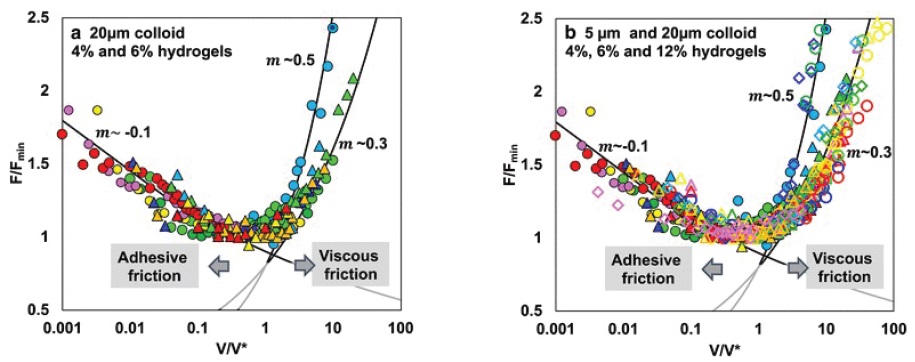Figure 2. Normalized friction force (F/Fmin) as a function of the normalized velocity (V/V*) for 4% (circles), 6% (triangles) and 12% (diamonds) hydrogels measured (a) with a 20-µm colloid and (b) with 20-µm (full symbols) and 5-µm (empty symbols) colloids. The black lines give F/Fmin∼(V/V*)m, with m∼−0.1 for the velocity-weakening friction regime and m∼+0.3 to +0.5 for the viscous regime. (Published with permission from Ref. 1.)
Such analytic models of hydrogel friction will put our understanding of these materials and their biological analogs on a firm theoretical footing. As an example, the model predicts that films with a less cross-linked outer layer supported by more highly cross-linked and therefore stiffer bulk should have low friction. Biological systems often exhibit such graded microstructures.
FOR FURTHER READING
1. Shoaib, T., Espinosa-Marzal, R.M. (2018), “Insight into the Viscous and Adhesive Contributions to Hydrogen Friction,”
Tribology Letters,
66, p. 96.
Eddy Tysoe is a distinguished professor of physical chemistry at the University of Wisconsin-Milwaukee. You can reach him at wtt@uwm.edu.
Nic Spencer is professor of surface science and technology at the ETH Zurich, Switzerland, and editor-in-chief of STLE-affiliated Tribology Letters journal. You can reach him at nspencer@ethz.ch.